SEGITIGA DAN SEGIEMPAT SMP/MTs KELAS 7
Segitiga
A. Jenis – jenis segitiga
Jenis-jenis segitiga dapat di tinjau dari besar sudut dan panjag
sisisnya
Segitiga berdasarkan besar
sudutnya
a. Segitiga lancip, yaitu segitiga yang
ketiga sudutnya lancip (00 – 900)
b. Segitiga Siku-Siku, yaitu segitiga yang
salah satu sudutnya adalah situ-siku atau (900)
c. Segiitga Tumpul, yaitu segitiga yang salah
satu sudutnya tumpul (900 – 1800)
 |
| SEGITIGA DAN SEGIEMPAT SMP/MTs KELAS 7 |
Segitiga ditinjau berdasarkan
panjang sisinya.
a. Segitiga
sama sisi, yaitu segitiga yang panjang ketiga sisisinya sama panjang.
b. Segitiga sama kaki, yaitu
segitiga yang mempunyai dua sisi yang sama panjang.
c. Segitiga sembarang, yaitu segitiga yang ketiga sisinya panjang nya
berbeda-beda (tidak ada yang sama panjang).
Contoh:
 |
| SEGITIGA DAN SEGIEMPAT SMP/MTs KELAS 7 |
B. Jumlah besar sudut-sudut segitiga
ABCD adalah persegi panjang
<A + <B
+ <C + <D = 900 + 900 + 900 + 900 =
3600
∆ ABD kongruen
dengan ∆ BCD
Jumlah sudut ∆
ABD = ∆ BCD
Maka jumlah sudut ∆ ABD = 1/2 x 3600 = 1800
Jadi jumlah besar sudut-sudut seitiga
adalah 1800
Contoh :
Di lihat dari sudut
dan panjang sisinya, segitiga PQR merupakan jenis segitiga apakah?
<PQR adalah sudut
lurus, pelurus 1000 adalah 800 (pelurus <SQR adalah
<PQR). Maka,
<P + < Q +
<R = 1800
<R = 1800 -
<P - <Q
<R =
1800 – 500
- 800
<R = 500
Pengecekan Konsep
1. Suatu
segitiga ABC, <A = 380, <B = 810 . tentukan !
a.
<C c. pelurus <B
b. pelurus <A d. <A + <B
2. Tentukan
jenis segitiga berikut, lancip, tumpul, situ-siku atau sama kaki.
a. 750, 280 c. 1100, 350
b. 590, 310 d 670, 580
3. Dari
∆ PLN , <P = (5x + 8)0, <L = (3x + 2)0, <N + (x
– 1)0, tentukanlah :
a. nilai x
b. Besar <P, <L, <N
4. Diketahui
∆ ABC, <A =(2x – 3)0, <B = (3x – 2)0, <C = (x
-1)0 , tentukanlah :
a. Nilai x
b. Besar
<A, <B, <C
|
C. Keliling dan Luas Segitiga
1. Keliling
K= S + S + S
K = AB + BC + AC
2. Luas Segitiga
Contoh:
1. Suatu segitiga PQR panjang sisinya PQ = 6 cm, QR = 8 cm dan PR = 10 cm tentukan keliling dan luasnya !
Jawab:
Diketahui : PQ = 6 cm, QR = 8 cm dan PR = 10 cm
K = S + S + S
K = PQ + QR + PR
K = 6 cm + 8 cm + 10 cm
K =
24 cm
2. Suatu segitiga luasnya 180 cm2,
jika tingginya 12 cm. Tentujkan panjang alasnya !
Jawab :
Diketahui : L = 180 cm2
, t = 12cm
D. Teorema Pythagoras dan Tripel
Pythagoras
Bunyi dalil Pitágoras = “Kuadrat sisi miring suatu segitiga sama dengan jumlah kuadrat dari sisi situ-sikunya”
Dari
persamaan tersebut dapat dibuat persamaan :
b2 = a2 – c2
c2
= a2 – b2
sedangkan tripel Pythagoras adalah tiga
(3) buah bilangan yang memenuhi syarat dalil pythagoras.
Contoh:
3, 4 dan 5 merupakan tripel pythagoras
karena 32 + 42 = 52
6, 8, dan 10 merupakan tripe; pythagoras
karena 62 + 82 = 102
5, 12 dan 13 merupakan tripel pythagoras
karena 52 + 122 = 132
| |
Pengecekan Konsep
1. Hitunglah Luas segitiga
siku-siku dengan panjang sisi siku-sikunya sebagai berikut:
a. 3
dan 4 cm c. 14 cm dan 17 cm
b. 6 cm dan 8 cm d. 5 cm dan 12 cm
2. Diketahui segitiga PQR luasnya 98 cm2, dan
panjang panjang QR = 4x. Tentukan !
a. Nilai x c. Panjang QR
b Panjang PQ
d. Panjang PR
|
Layang –layang PQRS dengan panjang diagonal QS = 10 cm, SR = 13 cm dan PS = 8 cm. Tentukan panjang diagonal PR !
4. Seorang anak menaikan
layang-layang dengan benang sepanjang 100m. Jika rentangan benang dianggap
lurus dan jarak anak ke titik di tanahh tepat di bawah layang – layanga adalah
80 m. Berapakah tinggi layang-layang?
5 Seorang anak berlari lurus dari tiik A ke titk B sejauh 30 m.
Kemudian dia berbelok kerah kanan di titik C sejauh 40 m. Berapa jarak
terdekat anak dari titik A ke titik C?
1. Bilangan Bulat Kelas 7 (LIHAT)
2. Bilangan Pecahan Kelas 7 (LIHAT)
3. Aritmatika Sosial Kelas 7 (LIHAT)
4. Contoh Soal Diagram Venn Kelas 7 (LIHAT)
5. Garis Dan Sudut Kelas 7 (LIHAT)
6. Materi Himpunan Kelas 7 (LIHAT)
7. Operasi-Operasi Himpunan Kelas 7 (LIHAT)
8. Penyajian Data Kelas 7 (LIHAT)
9. Perbandingan Kelas 7 (LIHAT)
10. Segitiga Segi Empat Kelas 7 (LIHAT)
11. Gradien Dan Persamaan Garis Lurus Kelas 8 (LIHAT)
12. Operasi Bentuk Aljabar Kelas 8 (LIHAT)
13. Persamaan Linier Dua Variabel Kelas 8 (LIHAT)
14. Relasi Dan Fungsi Kelas 8 (LIHAT)
15. Bilangan Berpangkat Kelas 9 (LIHAT)
16. Fungsi Kuadrat Kelas 9 (LIHAT)








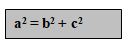



Belum ada Komentar untuk "SEGITIGA DAN SEGIEMPAT SMP/MTs KELAS 7 "
Posting Komentar