Materi FUNGSI KUADRAT Kelas 9 SMP/MTs
FUNGSI KUADRAT
1.
Fungsi
Kuadrat
kita sudah memahami apa yang dinamakan Fungsi pada materi sebeumnya, materi selanjutnya adalah Fungsi Kuadrat. Fungsi Kuadrat adalah suatu fungsi dengan pangkat tertingginya adalah 2 (dua) yang bisa disajikan dalam bentuk pasangan berurutan, tabel, diagram panah dan grafik.
Perhatikan beberapa fungsi dibawah ini:
a. f(x) = 2x2 – x + 3
b. f(x) = 3x – 2
c. f(x) = x3 – 2x
d. f(x) = 3x2 + 2x
pada bentuk persamaan diatas, persamaan (a)
dan (d) disebut fungsi kuadrat, sedangkan persamaan (b) dan (c) bukanlah fungsi
kuadrat.
Bentuk umum dari fungsi kuadrat:
f(x) = ax2 ± bx ± c, dengan a, b, dan c bilangan asli dan a≠ 0 |
Contoh soal:
Diketahui sebuah fungsi dengan rumus f(x) = x2
– 2x -3, dengan daerah asal { x| -2 ≤ x ≤ 4, x Є R}. tentukan:
a. Daerah
hasil
b. Nilai
dari f (-3)
Penyelesaian:
a.
Daerah hasil (kawan)
f(x)
= x2 – 2x - 3,
maka, f(-2) = (-2)2
– 2.(-2) – 3
= 4 – (-4) – 3 = 4 + 4 – 3 = 5
f(-1) =
(-1)2 – 2.(-1) – 3
= 1 – (-2) – 3 = 1 + 2 – 3 = 0
f(0) = (0)2 – 2.(0) – 3
= (0) – (0) – 3
= -3
f(1) = (1)2 – 2.(1) – 3
= 1 – 2 – 3 = -4
f(2) = (2)2 – 2.(2) – 3
= 4 – 4 – 3 = -3
f(3) =
(3)2 – 2.(3) – 3
= 9 – 6 – 3 = 0
f(4) =
(4)2 – 2.(4) – 3
= 16 – 8 – 3 = 5
Jadi daerah hasilnya
adalah {5, 0, -3, -4, -3, 0, 5)
b. Nilai f(-3)
f(x) = x2 – 2x – 3
maka:
f(-3) = (-3)2 – 2.(-3) – 3
= 9 – (-6) – 3 = 9 + 6 – 3 =12
Jadi nilai f(-3) adalah 12
1. Bilangan Bulat Kelas 7 (LIHAT)
2. Bilangan Pecahan Kelas 7 (LIHAT)
3. Aritmatika Sosial Kelas 7 (LIHAT)
4. Contoh Soal Diagram Venn Kelas 7 (LIHAT)
5. Garis Dan Sudut Kelas 7 (LIHAT)
6. Materi Himpunan Kelas 7 (LIHAT)
7. Operasi-Operasi Himpunan Kelas 7 (LIHAT)
8. Penyajian Data Kelas 7 (LIHAT)
9. Perbandingan Kelas 7 (LIHAT)
10. Segitiga Segi Empat Kelas 7 (LIHAT)
11. Gradien Dan Persamaan Garis Lurus Kelas 8 (LIHAT)
12. Operasi Bentuk Aljabar Kelas 8 (LIHAT)
13. Persamaan Linier Dua Variabel Kelas 8 (LIHAT)
14. Relasi Dan Fungsi Kelas 8 (LIHAT)
15. Bilangan Berpangkat Kelas 9 (LIHAT)
16. Fungsi Kuadrat Kelas 9 (LIHAT)
17. persamaan kuadrast kelas 9 (LIHAT)
Latihan soal 2.2
1. Dari
fungsi-fungsi dibawah ini, manakah yang merupakan fungsi kuadrat dan mana yang
bukan?
a.
f(x) = 4x2
+ 2x – 5
b.
f(x) = x
– 2x2
c.
f(x) = 4x
+ 3
d.
f(x) = x3
– 2x + 7
e.
f(x) = 3
– x – 5x2
2. Fungsi g
ditentukan oleh g(x) = 3x2 – 1
a.
Tentukan
nilai g(0), g(-1), g(1), g(-2) dan g(2)
b.
Jika g(x)
= 47 carilah nilai x
3. Fungsi kuadrat
f ditentukan dengan rumus f(x) = 4 + 2x – 3x2, tentukan nilai?
4. Diketahui
f(x) mx2 – (m+1)x + 3, jika nilai -b/a = 2, carilah
nilai m!
2.
Grafik
Fungsi Kuadrat
Contoh soal:
Gambarlah grafik fungsi kuadrat f(x) = x2
– 2x – 3 dengan daerah asal { x| -2 ≤ x ≤ 4, x Є R}.
Penyelesaian:
|
x |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
y |
5 |
0 |
-3 |
-4 |
-3 |
0 |
5 |
|
(x,y) |
(-2, 5) |
(-1, 0) |
(0, -3) |
(1, -4) |
(2, -3) |
(3, 0) |
(4, 5) |
Sedangkan grafik fungsinya adalah :
Dari grafik diatas, dapat diperoleh bahwa:
a. Pembuat nol fungsi adalah x = -1 dan x = 3
diperoleh jika f(x)=0 0 = x2 – 2x – 3
x2 – 2x – 3 = 0
(x + 1 ) ( x - 3) = 0
x + 1 = 0 dan atau x - 3 =0
x1 = -1 x2 = 3
jadi pembuat nol fungsinya x1= -1 dan x2 = 3
b. Persamaan
sumbu simetrinya adalah x =1
Persamaan sumbu simetri = (x1 + x2) : 2 = (-1 + 3) : 2 = 2: 2 = 1
jadi persamaan sumbu simetrinya adalah x = 1
c. Nilai
minimum fungsi aalah y = -4
nilai minimum dari sumbu simetri x = 1
maka`f(x) = x2 – 2x – 3
f(1) = 12 – (2. 1) – 3 = 1 - 2 - 3 = -1 - 3 = -4
jadi Nilai Balik minimun adalah -4
d. Koordinat
titik balik fungsi adalah (1, -4)
koordinat titik balik = (sumbu simsteri, nilaia minimun)
= (1, -4)
3. Diskrminan Persamaan Kudrat
Perhatikan bahwa √X merupakan bilangan real jika dan hanya
jika X ≥ 0. Karena selesaian persamaan kuadrat memuat
bentuk akar √(b2 – 4ac), bentuk
aljabar b2 – 4ac, yang
disebut diskriminan, akan menentukan sifat dan banyaknya
selesaian/akar dari persamaan kuadrat yang diberikan.
Untuk ax2 + bx + c =
0, dengan a ≠ 0,
1. Jika b2 – 4ac = 0, maka
persamaan kuadrat tersebut memiliki satu selesaian bilangan real.
2. Jika b2 – 4ac > 0, maka
persamaan kuadrat tersebut memiliki dua selesaian bilangan real.
3. Jika b2 – 4ac < 0, maka
persamaan kuadrat tersebut memiliki dua selesaian bilangan kompleks.
Contoh:
Menggunakan Diskriminan untuk Analisis Selesaian
Gunakan diskriminan untuk menganalisis
persamaan-persamaan kuadrat berikut apakah memiliki akar bilangan real. Jika
iya, nyatakan apakah akar-akar tersebut merupakan bilangan rasional atau
irasional, dan apakah persamaan kuadrat tersebut dapat difaktorkan atau tidak.
1. 2x2 + 5x + 2 = 0
2. x2 – 4x + 7 = 0
3. 4x2 – 20x + 25 = 0
Pembahasan
1. Persamaan
2x2 + 5x + 2 = 0
memiliki a = 2, b = 5,
dan c = 2. Sehingga,
Kita peroleh bahwa diskriminan dari persamaan kuadrat tersebut merupakan bilangan
kuadrat tidak nol. Maka persamaan tersebut memiliki 2 akar rasional dan dapat
difaktorkan.
2. Dari
persamaan x2 – 4x + 7 = 0 kita peroleh a = 1, b = –4,
dan c = 7.
Karena –12 < 0, maka persamaan kuadrat tersebut memiliki dua akar bilangan
kompleks dan tidak dapat difaktorkan.

3. Persamaan kuadrat 4x2 – 20x + 25 = 0 memiliki a = 4, b = –20, dan c = 25.
Maka,
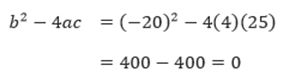
Perhatikan kembali contoh (2) di atas.
Diskriminan persamaan kuadrat pada contoh soal tersebut adalah –12, yang
berarti bahwa persamaan tersebut memiliki dua selesaian bilangan kompleks,
yaitu

Akar-akar tersebut dapat dituliskan sebagai x = 2 + √3 i dan x = 2 – √3 i, yang merupakan dua bilangan kompleks yang sekawan.
Semoga bermanfaat.






👍
BalasHapusTerimakasih banyak materi
BalasHapusThanks
BalasHapusThanks
BalasHapus